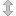Let us assume that the average kitchen pantry does not include such modern aeronautic oxidants and fuels such as liquid oxygen, hydrazine, etc. The average kitchen pantry does contain olive oil and oxygen however. Olive oil is a good fuel of choice for aeronautics, as it produces quite a bit of gas when combusted. The only factor that influences a fuel's ability to be a good rocket engine component is whether or not it moves mass out of the nozzle of the rocket when burned. Most other kitchen foods that our combustible, e.g. Cheetos, would not burn completely and would leave the rocket with uncombusted material, slowing the ascent of the rocket. Therefore, olive oil, or any other vegetable oil, makes a perfect choice.
Olive oil isn't just one chemical though; it is composed of 10 different acids, each with their own chemical properties when burned:

Olive Oil Components
Palmitic acid (7.5-20%)
Stearic acid (0.5-5.0%)
Arachidic acid (<0.6%)
Behenic acid (<0.3%)
Myristic acid (<0.05%)
Lignoceric acid (<0.2%)
Oleic acid (55-63%)
Palmitoleic acid (0.3-3.5%)
Linoleic acid (3.5-21.0%)
Alpha-linoleic acid (<1.0%)
Looking at the combustion reactions of these acids, one can calculate that for every 1 mole of olive oil that is burned, 9.364 mole of  and
and  are produced assuming complete combustion.
are produced assuming complete combustion.
The thrust force that is produced by an accelerating gas is calculated by the following equation:  where v is the exhaust velocity of the expanding gases and m is the mass flow rate of the gases.
where v is the exhaust velocity of the expanding gases and m is the mass flow rate of the gases.
Assuming that 1 mole of olive oil along with oxygen gas are burned in a 10 cm x 10 cm x 10 cm container every second, one can calculate the pressure of the gases inside the container.
On earth's surface: 
![v_e = \sqrt{\;\frac{T\;R}{M}\cdot\frac{2\;\gamma}{\gamma-1}\cdot\bigg[ 1-(p_e/p)^{(\gamma-1)/\gamma}\bigg]}](http://upload.wikimedia.org/math/c/c/a/cca069ad184645bb34245c48f95a4ff7.png)
where T=Temperature [K], R=8.314 J/(mol-K), M=Molecular Mass [kg/mol],  =Isentropic Expansion Factor of gas mixture,
=Isentropic Expansion Factor of gas mixture,  =Exhaust Pressure, P = Input pressure
=Exhaust Pressure, P = Input pressure
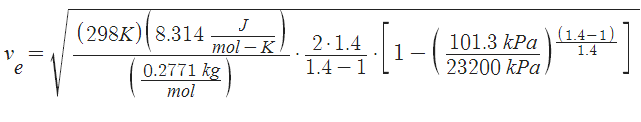
 so now we can calculate acceleration
so now we can calculate acceleration
 but mass changes instantaneously so perhaps we will have to use a different approach to find maximum velocity. Lucky for us, there's a solution:
but mass changes instantaneously so perhaps we will have to use a different approach to find maximum velocity. Lucky for us, there's a solution:
 If we burned the maximum amount of olive oil in order for the rocket to get off the ground, or 53.85 kg of olive oil (roughly 65.38 L or ~$520 worth) in a rocket shell that weighed roughly 5 kg, the max velocity would be
If we burned the maximum amount of olive oil in order for the rocket to get off the ground, or 53.85 kg of olive oil (roughly 65.38 L or ~$520 worth) in a rocket shell that weighed roughly 5 kg, the max velocity would be  . Escape velocity of earth is roughly 20x this quantity though (about 11200 m/s), but that's calculated at the surface. This rocket would surely not reach anywhere near that velocity, but it's maximum velocity would not occur at the surface, but rather high above the surface. Also the mass would change, so acceleration of the rocket would not be constant. Therefore, we must use calculus to determine the final height.
. Escape velocity of earth is roughly 20x this quantity though (about 11200 m/s), but that's calculated at the surface. This rocket would surely not reach anywhere near that velocity, but it's maximum velocity would not occur at the surface, but rather high above the surface. Also the mass would change, so acceleration of the rocket would not be constant. Therefore, we must use calculus to determine the final height.


Graph of acceleration as a function of time:
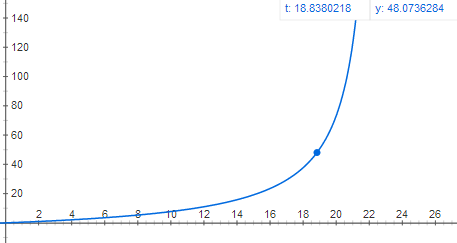

1295.6 m is roughly 1/100 the way to space, not even including air resistance. Perhaps your dreams of amateur rocketry have been dashed by the laws of physics once again...

"But wait!" you might say. "You could try launching it from an asteroid, where the gravity is so much less!" But this wouldn't work, as most kitchens are not found on asteroids, but on the off chance that a kitchen found itself on a rocky outgrowth of the far solar system, we'll explore this phenomenon anyways. In this case, the air resistance would be so negligible anyways, that there would be no noticeable effect from neglecting it entirely.
Of course, choosing a new planet would mean a new escape velocity as well as a new gravitational force, which brings us back to the drawing board. Assuming an asteroid with radius 1 km and mass  (a density approaching that of Earth or any of the other terrestrial planets), the new gravitational acceleration on the rocket would be
(a density approaching that of Earth or any of the other terrestrial planets), the new gravitational acceleration on the rocket would be  definitely more manageable for a lowly olive oil rocket to manage and definitely more allowing for a larger mass of olive oil to be burned. Assuming that at the beginning, all of the force of thrust is being used to counteract the mass of the olive oil and rocket:
definitely more manageable for a lowly olive oil rocket to manage and definitely more allowing for a larger mass of olive oil to be burned. Assuming that at the beginning, all of the force of thrust is being used to counteract the mass of the olive oil and rocket:
 where x = number of kg of olive oil
where x = number of kg of olive oil
 or roughly 8000x as much as on Earth. But that's not including oxygen, which this asteroid's "atmosphere" is sure not to contain. To oxidize 1 kg of olive oil's combustion requires 2.708 kg of oxygen. Therefore, the correct expression would really be
or roughly 8000x as much as on Earth. But that's not including oxygen, which this asteroid's "atmosphere" is sure not to contain. To oxidize 1 kg of olive oil's combustion requires 2.708 kg of oxygen. Therefore, the correct expression would really be
 as each kg of olive oil adds 2.708 kg of oxygen extra.
as each kg of olive oil adds 2.708 kg of oxygen extra.
Under this expression, the maximum amount of olive oil would be  or roughly 2000x as much as on Earth. Thus, we can now calculate acceleration.
or roughly 2000x as much as on Earth. Thus, we can now calculate acceleration.


Graph of acceleration as a function of time (much slower acceleration but for a much longer period of time)
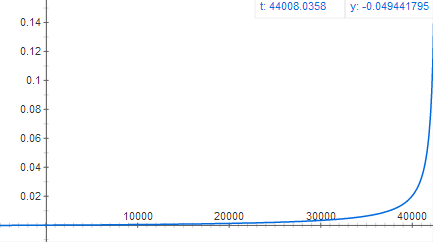

 when oil is finished burning. At that height,
when oil is finished burning. At that height,

In order for a rocket to remain in orbit at that altitude, it must have a minimum speed. To calculate that minimum speed, one must use:
 which is well below the calculated speed of the rocket. Therefore, the rocket would be considered in orbit, and thus successful.
which is well below the calculated speed of the rocket. Therefore, the rocket would be considered in orbit, and thus successful.
One must of course remember that in order for this rocket to work, one would have to transport 110000 kg of olive oil along with 297880 kg of oxygen to an asteroid very far away from Earth, quite the unfeasible task. In essence, yes it is possible to make a rocket that works with nothing other than what you would find in your kitchen, but the parameters under which it would have to work would be impossible for the average person to accomplish in their kitchens. Perhaps, hold off your mass purchases of olive oil in hope of some amateur rocketry for another day.
Works Cited
 icons at the top right corner of the subsection.
icons at the top right corner of the subsection.