I. Data & Analysis
Data (Part A)
Color #1: violet
|
% transmission
|
Stopping potential (V)
|
Approx. charge time (s)
|
|
100
|
2.10
|
2
|
|
80
|
1.96
|
2
|
|
60
|
1.96
|
3
|
|
40
|
2.07
|
3
|
|
20
|
2.04
|
4
|
Color #2: green
|
% transmission
|
Stopping potential (V)
|
Approx. charge time (s)
|
|
100
|
.75
|
1
|
|
80
|
.77
|
1
|
|
60
|
.73
|
1
|
|
40
|
.75
|
1
|
|
20
|
.70
|
1
|
Data (Part B)
|
Color
|
Stopping potential (V)
|
Frequency (x1014 Hz)
|
Wavelength (nm)
|
|
Yellow
|
.66
|
5.2
|
577
|
|
Green
|
.72
|
5.5
|
545
|
|
Blue
|
1.41
|
6.9
|
435
|
|
Violet
|
1.60
|
7.3
|
411
|
|
Ultraviolet
|
1.94
|
8.2
|
366
|
Analysis (Exp 1)
1. The intensity of the light had very little effect on the stopping potential of the circuit, and therefore little effect on the maximum energy of the photoelectrons. As intensity decreased, the recharge time increased somewhat.
2. The higher the frequency of light, the higher the stopping potential. So a higher frequency of light means that the photoelectrons have a greater maximum energy.
3. This experiment supports a quantum model of light, since the intensity seems to have no effect on the energy of light (which would be the case if light were a wave), but the frequency does have an effect (which would not be the case if light were a wave).
4. Some charge is always leaking off, which decreases the voltage. At lower intensities, the supply of photoelectrons isn’t replenished as quickly (since there are fewer photons available), so the light can’t maintain as high a charge (and therefore as high a voltage) as before.
Analysis (Exp 2)
1. Determine the frequency and wavelength of each spectral line.
Sample calc:
λf = c
λ = c/f = (3x108 m/s)/(5.2x1014 Hz) = 577 nm
2. Determine h, W0
Stopping Potential vs. Frequency
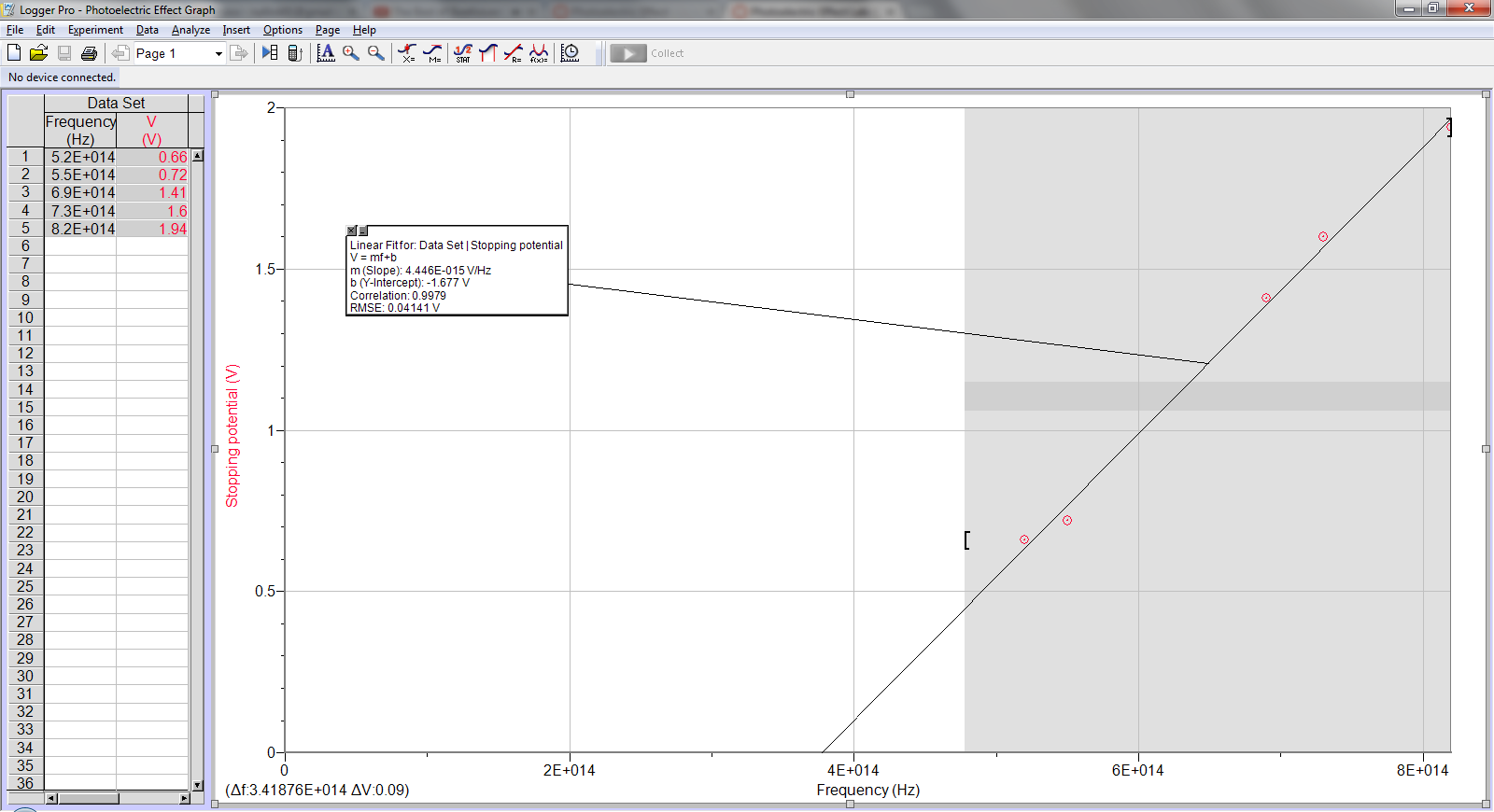
Line of best fit: y = (4.45e-15)x – 1.68
E = W0 + K
hf = W0 + qVstop
Vstop = (h/e)f – W0/e
So m = h/e and b = W0/e
h = em = (1.602e-19C)(4.45e-15 V/Hz) = 7.13e-34 J-s
W0 = -eb = (1.602e-19 C)(1.68 V) = 2.69e-19 J
II. Discussion questions
1. If light striking the phototube acts like a wave, would you expect the stopping voltage to depend on the frequency of the light?
No. The energy of a wave is independent of its frequency, so the energy of the photoelectrons, and therefore the stopping voltage, would not be affected by the frequency.
2. If light striking the phototube acts like a wave, would you expect the stopping voltage to depend on the intensity of the light?
Yes. The energy of a wave depends on its intensity, so the energy of the photoelectrons, and therefore the stopping voltage, would depend on the intensity.
3. If light striking the phototube acts like a wave, would you expect a time delay between the time that light strikes the emitter and the emission of photoelectrons?
No. The wave would exist everywhere around the emitter, and so it would be able to reach and energize the electrons pretty much instantaneously.
4. If light striking the phototube acts like a stream of particles, would you expect the stopping voltage to depend of the frequency of the light?
Yes. The energy of light particles does depend on its frequency, and so the energy of the electrons (and the stopping potential) would depend on the frequency.
5. If light striking the phototube acts like a stream of particles, would you expect the stopping voltage to depend on the intensity of the light?
No. If light is a particle, then the energy of each individual particle does not depend on the intensity (i.e. number of particles), and so the energy of the electrons (and the stopping potential) would be unaffected by intensity.
6. If light striking the phototube acts like a stream of particles, would you expect a time delay between the time that the light strikes the emitter and the emission of photoelectrons?
No. If light is a particle, there are still many, many light particles hitting the phototube, and since electrons are excited by collision with a photon, many electrons would be emitted immediately. If the number of light particles was reduced, though, it would take longer the emitted electrons to accumulate and reach the stopping potential.
7. Wave or quantum model?
This experiment supports a quantum model of light. The stopping potential was unrelated to the intensity of the light, but it was linearly related to the frequency of the light. As a result, the energy of the ejected electrons was related to frequency but not intensity. This is more consistent with a quantum model of light.
 icons at the top right corner of the subsection.
icons at the top right corner of the subsection.