Rifle Toss:

            Being on North’s Color Guard, I’ve come to notice that people’s favorite piece of equipment to watch be used is the rifle. Specifically, people like to watch me toss rifle because as a male, I have much more muscle mass than your typical girls that populate color guard teams which allows me to perform tosses that far exceed the abilities of my teammates. (It’s just a fact, I’m not being arrogant or anything, I promise)  While watching a guy throw a wood rifle over 3 meters up into the air is amazing to watch, how much energy must a person be able to put out in order to perform one of these tosses?

 

 

Key Values to Know-

  Toss Rotations: 8                            

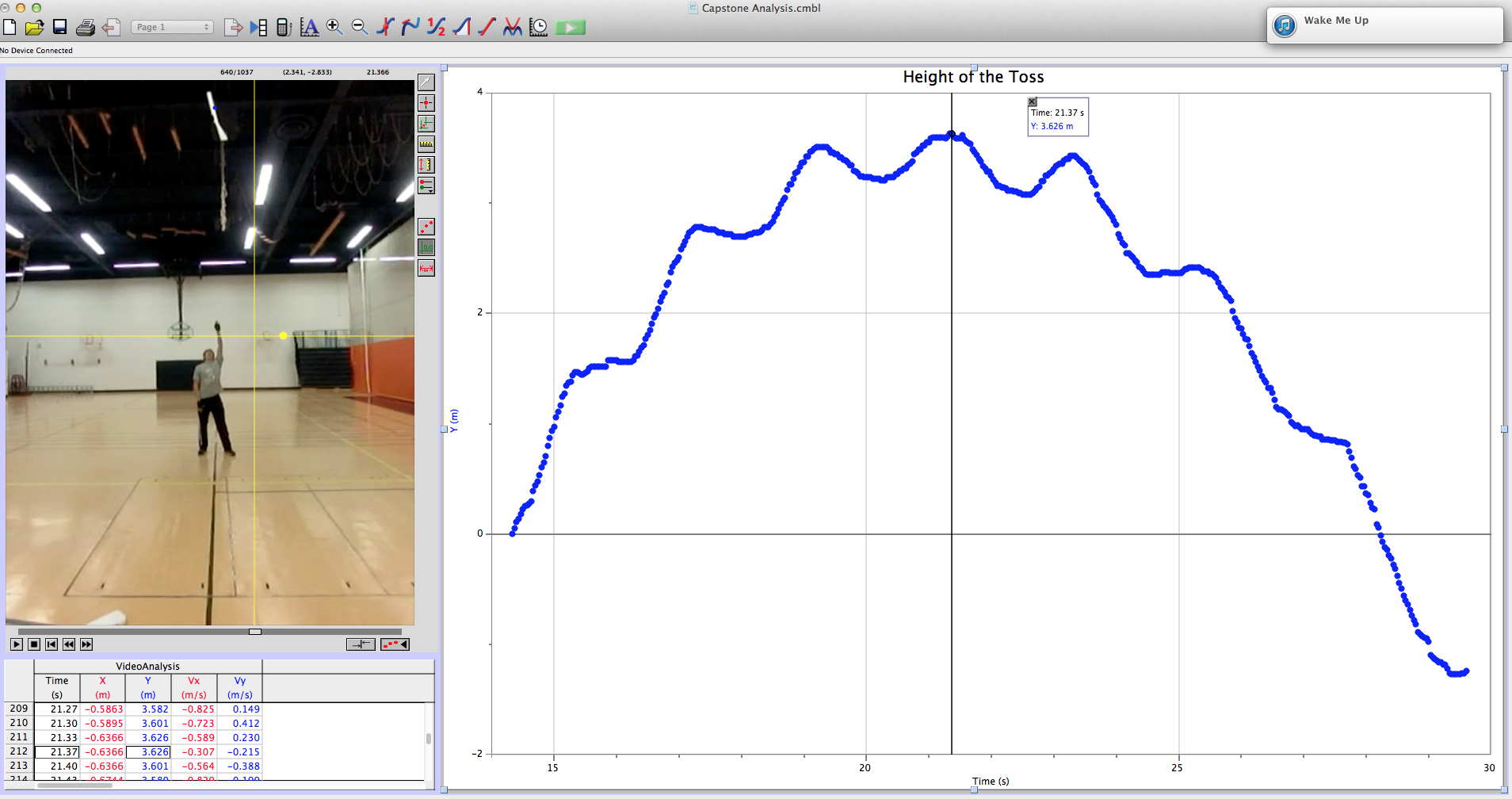
  Height of the toss: 3.6 meters       

  Mass of the rifle: 1.076 Kg

 The toss height was found with video analysis in LoggerPro

Assumptions-

Negligible air resistance

Negligible friction for contact with hands

 

Intro:

 

Before starting, tossing a guard rifle is by no means as simple as it may appear to be through this project.  It does take practice get tosses correct.  In this experiment, the total is a combination of that exerted by both hands since it’s very difficult to toss a rifle with just one hand.  I treated it as though a single contact, one hand, was used to input the energy into my rifle system.

 

Energy Analysis-

Looking at the system for the rifle, it’s not very complex.  At the start of the toss, the rifle has no energy except the small amount of gravitational potential energy being about a meter off the ground.  Energy is first put into the system when I push down on the butt of the rifle, supplying the needed energy for the rotation.  Secondly, my hand along the neck of the rifle pulls up, inputting the kinetic energy needed to achieve the required height which is converted into potential at its peak height.  Since we are assuming that we have a perfect system, all of the kinetic should eventually be converted into potential.

 

 

Here’s where the fun begins!

 

So from this, you can find the total energy of the system at the peak of the toss…

 

If you’re wondering what that new equation at the back half is, here’s your answer.  We already learned about what regular kinetic and potential energy are, but now you get to learn about a new one, which is Rotational Kinetic Energy.  This, obviously, applies only when an object is undergoing rotation within its system.

 

 

I: Moment of Inertia, : Angular Velocity

 

Angular velocity:

 

f: frequency of the toss = 1.5296 rev/sec

 

 

 

 

As some of you may know, Mr. Schmit and I spent a couple days attempting different experiments to solve for the second half of the Rotational Energy equation.  The problem with my rifle was that it isn’t a uniformly distributed object with reference to its mass, but finally an accurate solution was found.  By creating a pendulum from the rifle, you can solve for any object’s Moment of Inertia

 

Parallel Axis Theorem:

 

 

 

 : Moment of Inertia at the Pivot Point, : Moment of Inertia at the Center of Mass, M: mass, : distance from pivot point

 

But don’t worry; this isn’t the actual form of the equation wanted.  Taking this equation, it is later on derived into another one that better suits the needs for this experiment by matching it with SHM (Simple Harmonic Motion).

 

 

: Moment of Inertia at the Center of Mass, M: mass, : distance from pivot point, T: Period of the object, g: acceleration due to gravity

Period of a Pendulum:

 

L: length of pendulum, g: acceleration due to gravity

 

Solving for , you get

 

 

 

 

Now with the two missing variables found, finding the total energy put into the system is easy.

 

 

 

        3.518

               

 

So I expend about 42 Joules of energy each time I toss an 8, not too shabby.

But wait!  Let’s say that you were to try tossing this each of the planets in the solar system, how much energy would be required?

 

A Trans-Celestial Performance:

 

To figure the energy needed to toss on each of the planets, the only change that would need to be made is the acceleration due to gravity in the past equations , which can be found for any two masses with Newton’s Law of Gravitation.

 

 

 

G: Universal Gravitational Constant (), M: mass of an object or planet, r: radius from center of planet to object

Then Force of gravity equation, you can solve for the acceleration due to gravity.

 

 

 

M: mass of the object, g: acceleration due to gravity

 

 

Planet	Mass (kg)	Radius (m)
Mercury	3.30 x 10ˆ23	2,440,000
Venus	4.87 x 10ˆ24	6,051,000
Earth	5.97 x 10ˆ24	6,378,000
Moon	7.35 x 10ˆ22	1,738,000
Mars	6.42 x 10ˆ23	3,397,000
Jupiter	1.90 x 10ˆ27	71,492,000
Saturn	5.69 x 10ˆ26	60,268,000
Uranus	8.66 x 10ˆ25	25,559,000
Neptune	1.03 x 10ˆ26	24,764,000
Pluto	1.31 x 10ˆ22	1,160,000

 

And other favorite solar bodies

Sun	1.989 x 10^30	695,500,000
M87 Black Hole	1.19 x 10^40	1.93 x 10^13
Neutron Star	6.365 x 10^30	12,000

 

After the calculations, the acceleration values are as follow…

Solar Body	()
Mercury	3.61
Venus	8.83
Earth	9.8
Moon	1.6
Mars	3.75
Jupiter	26
Saturn	11.2
Uranus	10.5
Neptune	13.3
Pluto	.65
Sun	274.13
M87 Black Hole	2130.87
Neutron Star	2.94 x 10^12

 

Substitute these in place of Earth’s gravitational acceleration in the equations from Energy, Period of a Pendulum, and Parallel Axis Theorem to adjust for the new gravity and VOILA, you have your required energy outputs for the toss!

 

But I don’t think you really want to read through all of them so here are the final results.

Solar Body	()
Mercury	21.06
Venus	41.408
Earth	41.627
Moon	13.286
Mars	21.65
Jupiter	108.065
Saturn	50.58
Uranus	47.86
Neptune	58.73
Pluto	17.86
Sun	1071.89
M87 Black Hole	8952.39
Neutron Star

 

That Neutron Star:

 

Let’s take another look at our buddy, Neutron Star.  What this value means is that it takes a person over 11 trillion Joules of energy to toss an eight-rotation toss.  Written out, that’s 11,420,043,700,000 Joules.  So one essentially needs explode approximately one kiloton of TNT or a mini nuclear fusion bomb and covert all of that energy from the explosion directly into mechanical energy input for this toss.

 

That energy is the equivalent to eating any of the following:

 

• 28,700,000,000 apples
• 25,900,000,000 bananas
• 2,720,000,000 watermelons
• 13,990,000,000 Chocolate Donuts
• 4,960,000,000 Big Macs
• 14,300,000,000 McNuggets
• 5,450,000,000 Large Fries

 

Now, the last question that must be posed is how many rotations would a toss of that energy on Earth be because why wouldn’t you want to know. So, let’s start working backwards.

 

 

 

Since a toss of this magnitude surely would want a greater height to show off to the audience, the height will change to 13 meters, which is about the height of a football goal post.  Gravity and  will change back to Earth’s values, and it will be assumed that the toss takes the same amount of time, 5.23 seconds.

 

 

 

 

 

 

 

Taking this time value, multiply the revolution of the toss per second by this time to get the total rotations from the initial energy input.

 

 

 

Thanks to:

 

"Parallel Axis Theorem." Wikipedia. Wikimedia Foundation, 12 July 2013. Web. 17 Dec. 2013.

 

"Rotation around a Fixed Axis." Wikipedia. Wikimedia Foundation, 12 Sept. 2013. Web. 17 Dec. 2013.

 

"Projectiles." - The Physics Hypertextbook. N.p., n.d. Web. 17 Dec. 2013.

 

"Gravitation." Wikipedia. Wikimedia Foundation, 15 Dec. 2013. Web. 15 Dec. 2013.

 

"List of Solar System Objects by Size." Wikipedia. Wikimedia Foundation, 18 Dec. 2013. Web. 17 Dec. 2013.

 

"Neutron Star." Wikipedia. Wikimedia Foundation, 17 Dec. 2013. Web. 17 Dec. 2013.

"Supermassive Black Holes." Supermassive Black Holes. N.p., n.d. Web. 17 Dec. 2013.

 

Lastly, a huge thanks to Mr. Schmit and his physics professor friends, who without, this project wouldn’t have been able to be finished.